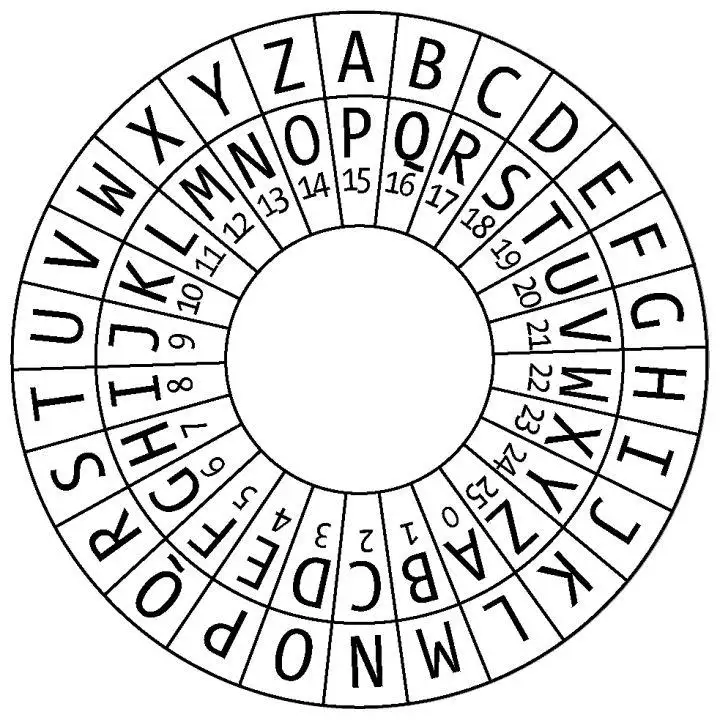
凯撒密码技术是最早、最简单的加密技术之一。它只是一种替换密码，即给定文本的每个字母都被字母表中一些固定位置的字母替换。例如，移位为 1，A 将被 B 替换，B 将变为 C，依此类推。该方法显然是以朱利叶斯凯撒命名的，他显然用它来与他的官员交流。
因此，为了加密给定的文本，我们需要一个整数值，称为 shift，它表示文本中每个字母被向下移动的位置数。
加密可以使用模算术表示，首先将字母转换为数字，根据该方案，A = 0，B = 1，...，Z = 25。通过移位 n 对字母的加密可以在数学上描述为。

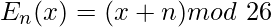
（移位 n 的加密阶段）

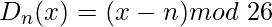
（带移位 n 的解密阶段）

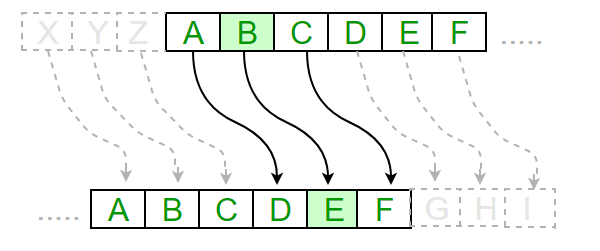
例子 ：

文本：ABCDEFGHIJKLMNOPQRSTUVWXYZ
移位：23
密码：XYZABCDEFGHIJKLMNOPQRSTUVW

文本：ATTACKATONCE
移位：4
密码：EXXEGOEXSRGI

凯撒密码算法：
输入：

一串小写字母，称为文本。
一个 0-25 之间的整数，表示所需的移位。
程序：

一次一个字符地遍历给定的文本。
对于每个字符，根据我们是加密还是解密文本，按照规则转换给定的字符。
返回生成的新字符串。
接收文本（字符串）和移位值（整数）并返回加密文本的程序。

C++

// A C++ program to illustrate Caesar Cipher Technique

include <iostream>

using namespace std;

// This function receives text and shift and
// returns the encrypted text
string encrypt(string text, int s)
{

string result = "";

// traverse text
for (int i=0;i<text.length();i++)
{
    // apply transformation to each character
    // Encrypt Uppercase letters
    if (isupper(text[i]))
        result += char(int(text[i]+s-65)%26 +65);

// Encrypt Lowercase letters
else
    result += char(int(text[i]+s-97)%26 +97);
}

// Return the resulting string
return result;

}

// Driver program to test the above function
int main()
{

string text="ATTACKATONCE";
int s = 4;
cout << "Text : " << text;
cout << "\nShift: " << s;
cout << "\nCipher: " << encrypt(text, s);
return 0;

}

Python3

#A python program to illustrate Caesar Cipher Technique

def encrypt(text,s):

result = ""

# traverse text
for i in range(len(text)):
    char = text[i]

    # Encrypt uppercase characters
    if (char.isupper()):
        result += chr((ord(char) + s-65) % 26 + 65)

    # Encrypt lowercase characters
    else:
        result += chr((ord(char) + s - 97) % 26 + 97)

return result

check the above function

text = "ATTACKATONCE"
s = 4
print ("Text : " + text)
print ("Shift : " + str(s))
print ("Cipher: " + encrypt(text,s))

如何解密？
我们可以编写另一个类似于 encrypt 的函数 decrypt，它将向相反方向应用给定的移位来解密原始文本。但是我们可以在模下使用密码的循环属性，因此我们可以简单地观察

密码（n）=解密（26-n）